Filter Wheel Alignment

program names, file names
variable names
prompts, commands, program code

Tables:
  1. CVF specs

  2. hydrogen transitions

  3. Sample data

  4. Filter wheel software parameters

The filter wheel in the University of Rochester 3rd Generation Infrared Camera has six broadband and three narrowband filters. Each of the narrowband filters is a circular variable filter (CVF), such that each point along a CVF acts as a narrowband filter (~2% resolution at near-infrared wavelengths), and transmission wavelength is a function of position along the filter. Click here to see a schematic diagram of the filter wheel. Below is a table giving approximate characteristics of the three CFVs:

Table FW1: CVF specs
name minimum wavelength* maximum wavelength* short-wavelength end
(filter wheel position)
CV0 ("J-H band") 1160 nm 2270 nm 7223.88
CV1 ("K band") 1850 nm 2790 nm 4446.08
CV2 ("L band") 2325 nm 4575 nm 1668.28
*approximate value

The filter wheel is rotated by a small electric motor (the "stepper motor") mounted on the side of the camera. The stepper motor moves the filter wheel by angular steps called "filter wheel positions". The last column of the above table gives the filter wheel position of a particular point on each CVF. 10,000 filter wheel positions corresponds to a full 360° rotation. Each CVF has an angular length of 90°, so it takes 2500 filter wheel positions to move from one end of a CVF to the other end.

For the stepper motor and filter wheel to work properly, the computer which operates the camera must know the orientation of the filter wheel at a given moment, and by how much to rotate the filter wheel in order to put the correct filter into the camera's optical path. The filter wheel must therefore be carefully calibrated before observing. We generally do a thorough calibration in the lab before leaving for the observatory, with occasional spot-checks of the alignment during the observing run.

The initial alignment is done using a hydrogen lamp -- a long glass tube filled with hydrogen gas which is stimulated electrically. The lamp is placed under the camera such that the tube is as near as possible to the focus of the camera lens -- this takes a bit of fiddling, but here are a couple of rough estimates: there should be about 10" between the hydrogen lamp tube itself and the dewar baseplate when using the WIRO lens, and there should be about 2.5" between the hydrogen lamp tube itself and the dewar baseplate when using the MLOF lens.

The idea here is to take lots of images of the hydrogen lamp at a sequence of wavelengths such that an atomic transition of hydrogen falls within this wavelength interval. Then, knowing the rest wavelength of the transition, and making a plot of intensity v. filter wheel position, you can determine the filter wheel position corresponding to the wavelength of the hydrogen transition (the intensity increases as you go through the transition, and then drops back down after passing it).

We usually start about 100 filter wheel positions away from the nominal filter wheel position of the transition, and then walk the filter wheel through the transition (we typically step the filter wheel by 10 positions between images). This should be done as quickly as possible, because the glass of the tube gets very hot, and this complicates doing the photometry. It's a good idea to walk the filter wheel through one transition, and then to turn off the lamp and wait for a few minutes before starting again. And, for each set of images, it's important to go far enough past the atomic transtition that the intensity profile falls back down near the baseline value.

Images of the lamp should look something like this:

The bright narrow horizontal stripe in the middle is the hydrogen gas in the lamp tube, and the broader, fainter stripe is the glass of the tube (the outer diameter of the glass tube is eight or nine times the diameter of the inner gas-filled region). The boxes show likely places to put photometry boxes.

We usually do photometry at three points along the tube, as seen by the lower three boxes on the gas-filled part of the tube (the "source boxes"). Additionally, we need to do a background subtraction with photometry boxes (the "background boxes") near the source boxes, such that the background boxes are away from the hydrogen gas but still on the glass tube. There are utilites in the data-acquisition software that do this photometry for you. These utilities return box totals, rather than box means, so make sure that each background box is the same size as its corresponding source box (otherwise you'll have to rescale the box totals according to box size).

Once you've got all the box totals, do the background subtractions and make a plot of intensity v. filter wheel position for each. Then you can just use fwhm to find the peak's centroid. You should get something like this:

[output plot of fwhm.pro]

The centroid of the profile is printed at the top of the fwhm plot. This is the measured filter wheel position for the transition wavelength.

The software used to rotate the filter wheel assumes a linear relationship between wavelength and filter wheel position. So, ideally, you should do two wavelengths for each CVF (because two points determine a line). This is possible for CV0 and CV1, but the backgroud emission gets so high at longer wavelengths, that (in my experience) there is only one sufficiently bright hydrogen transition that falls within the wavelength range of CV2 and can be measured with the hydrogen lamp we use here in the lab. Below is a table of the transitions we typically use:

Table FW2: hydrogen transitions
transition CVF approximate filter
wheel position		 wavelength
Paschen beta 0 6960 1282 nm
Brackett gamma 0 4960 2166 nm
Brackett gamma 1 3610 2166 nm
Brackett beta 1 2390 2626 nm
Brackett beta 2 1330 2626 nm

Let's assume that after taking the data (and after taking the average filter wheel position for each box at each transition), you get the following results:

Table FW3: sample data
transition CVF approximate filter
wheel position		 wavelength
Paschen beta 0 6955 1282 nm
Brackett gamma 0 4955 2166 nm
Brackett gamma 1 3605 2166 nm
Brackett beta 1 2385 2626 nm
Brackett beta 2 1330 2626 nm

Let's calculate the parameters of the linear relationship between wavelength and filter wheel position for CV0. First the slope:
The name of the corresponding software parameter is 0.slope, and it is expressed AS AN INTEGER in units of 10-3 nm/fwp:
0.slope = -440

Having the slope allows us to calculate the intercept bo:
bo = 4345.2 nm

Using the filter wheel position of the short-wavelength end of CV0 (given in Table FW1 as Fo = 7223.88), we can compute the corresponding wavlength of that end. This software parameter is called 0.L0, and it is expressed as an integer in nanometers:
0.L0 = mo Fo + bo = 1167 nm

Now, knowing that a CVF is 2500 filter wheel positions long, we can compute the wavelength of the other end of cv0:
0.Lmax = mo * (Fo - 2500) + bo = 2267 nm

Now we do the same thing for CV1, using Fo = 4446.08 (from Table FW1):

1.slope = -377
b1 = 4345.2 nm
1.L0 = m1 Fo + b1 = 1849 nm
1.Lmax = m1 * (Fo - 2500) + b1 = 2790 nm

Finally, for CV2, since we have only one point, we'll assume 2.slope = -900 (which means that m2 = -0.900 nm/fwp). Using this with our measurement gives the intercept b2:
b2 = 3823.0 nm

Table FW1 tells us that Fo = 1668.28 for CV2:
2.L0 = m2 Fo + b2 = 2322 nm
2.Lmax = m2 * (Fo - 2500) + b2 = 4572 nm

These calculations are the actual numbers for the apr99wiro observing run. They are reproduced below, along with the numbers for three other recent observing runs.
Table FW4: Filter wheel software parameters
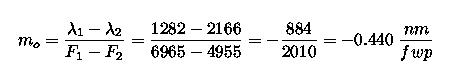
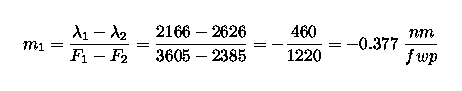
parameter oct98mlof apr99wiro oct99wiro apr00wiro
0.slope -439 -440 -445 -440
0.L0 1176 1167 1160 1159
0.Lmax 2282 2267 2274 2265
1.slope -379 -377 -376 -372
1.L0 1848 1849 1854 1860
1.Lmax 2794 2790 2793 2791
2.slope -900 -900 -900 -900
2.L0 2318 2322 2326 2322
2.Lmax 4573 4572 4578 4573

These numbers should be entered into the the filter wheel file. As of this writing (11 August 2000), we are using Filter Wheel V (V as in 5). The name of the file is filterV.fts, and it's probably in /applic/runtime/fwheels/ on the data computer. The filter wheel positions for the short-wavelength ends of the CVFs 0.Fw0, 1.Fw0, and 2.Fw0 (the numbers given in the last column of Table FW1) are also in this file --- never, ever, ever change these parameters in the file under any circumstances.

Finally, as mentioned above, we sometimes also spot-check the alignment of the filter wheel while on an observing run. One way to do this is to pick a broadband filter (the K-band filter is good for this) and walk through the filter at 10-step increments, computing a box mean or box total at each step. Plotting intensity v. filter wheel position should give a fairly symmetric, centrally-peaked function, the centroid of which is the central filter wheel position of that filter. The overall angular orientation of the filter wheel can then easily be updated in the software so that the center of the broadband corresponds to one of the following numbers (expected by the software): J at 8890, H at 8610, K at 8335, 3.3 at 8055, L'' at 7780, and M' at 7500.

Carl Welch